Où allons-nous?
Jules Delisle, révision Mario Lessard 2016
Où allons-nous?
En astronomie, comme dans toutes les sciences naturelles, l'observation (ou l'expérimentation) se conjugue avec la théorie dans l'élaboration de nos connaissances. L'une et l'autre contribuent à l'avancement des sciences. Certaines théories ont permis de faire des pas de géant ou de réduire à néant des théories acceptées depuis longtemps.
On peut citer les théories de la relativité d'Einstein qui ont révolutionné la façon d'aborder les problèmes de la physique. L'observation, en astronomie, a permis certains développements importants bien avant que la théorie ne puisse expliquer les phénomènes observés. On pense ici à Kepler, qui a découvert les principales caractéristiques du mouvement des planètes bien avant que Newton n'énonce les lois qui permettent de calculer leur trajectoire. Il arrive aussi que les observations viennent remettre en cause des théories acceptées par la plupart des membres de la communauté scientifique.
Ce pourrait à nouveau être le cas avec la découverte des savants du groupe "High-Z Supernova Search Team" (HZSST) [ainsi que celle du "Supernova Cosmology Project" (SCP)]. Ils ont mesuré les vitesses d'éloignement de supernovæe lointaines. Ils ont trouvé que, contrairement à la théorie, ces vitesses croissent avec le temps, c'est-à-dire qu'elles sont soumises à une force d'accélération alors que la théorie prévoit que ces vitesses décroissent sous l'effet de la gravité. En annonçant ce résultat, [le responsable de l'équipe du HZSST], Brian Schmidt, n'a pu se retenir de dire : "Ma propre réaction en est une d'étonnement et d'horreur". Étonnement, parce qu'il ne s'attendait pas à un tel résultat et, horreur, sans doute, face à la perspective des débats qu'il devrait affronter avec de tels résultats qui remettaient en question plusieurs des hypothèses à la base des théories sur l'évolution de l'Univers. [Aujourd'hui, on sait que ces données ont été confortées aussi par l'analyse du fond cosmologique avec la mission "WMAP", ainsi que par les données reliées aux oscillations baryoniques acoustiques. Il y a donc un consensus: une énergie sombre accélère bel et bien l'expansion de l'Univers.]
Pour expliquer une telle accélération des [galaxies], il est nécessaire qu'elles soient soumises à une "force antigravitationnelle" [dont la réalité échappe aux cosmologistes]. Le problème, c'est qu'une telle force ne fait pas partie du bagage des lois avec lesquelles les physiciens essaient d'expliquer l'évolution de l'Univers. Cependant, ce n'est pas la première fois qu'on mentionne la possibilité d'une force de cette nature. Un retour en arrière nous permet de constater qu'elle a une histoire intéressante.
C'est en 1916 qu'Einstein a énoncé la théorie de la relativité générale dont l'originalité consistait à remplacer la gravité par une ["pseudo-force"] qui était liée aux propriétés de l'espace. Ceci l'amenait à décrire l'espace par un ensemble d'équations. Ces équations lui posaient un problème qui l'embarrassait. En effet, la solution de ces équations conduisait nécessairement à conclure que l'Univers ne pouvait pas être stable. À l'époque, ceci paraissait inconcevable comme hypothèse scientifique et Einstein n'osa pas défier cette croyance générale. Pour rendre sa théorie conforme aux idées du temps, il ajouta une constante à ses équations, qu'il appela “constante cosmologique”. Celle-ci représentait, en pratique, une force antigravitationnelle.
Je ne peux m'empêcher de m'arrêter pour faire remarquer jusqu'à quel point nos conceptions ont pu évoluer depuis 80 ans. Même un savant de la stature d'Einstein, dont les théories devaient révolutionner notre connaissance du monde n'a pas osé s'attaquer à cette croyance en un Univers aux dimensions stables. On peut penser que sa nouvelle théorie était tout à fait révolutionnaire et qu'il craignait qu'elle ne soit discréditée parce qu'elle conduisait à une telle conclusion. Peut-être que cela lui paraissait tellement excessif qu'il ne voulait pas mettre ainsi en péril sa réputation. Einstein était déjà bien connu, car il avait déjà à son crédit la théorie de la relativité restreinte, qu'il avait énoncée en 1905. De toute façon, on peut penser qu'il était alors dangereux de soutenir que l'Univers était en expansion.
Au cours des années 1920, cette croyance allait être sérieusement bouleversée. En premier lieu, un savant russe, Alexandre Friedmann, démontra que même l'ajout de la constante cosmologique ne permettait pas d'obtenir un Univers stable comme solution aux équations de la relativité générale. Il fut d'ailleurs l'un des premiers à proposer le modèle d'un Univers en expansion. De plus, c'est au cours de cette décade que Hubble et son équipe firent les découvertes qui devaient l'immortaliser. Il fit la mesure de la distance des nébuleuses et établit que certaines sont des galaxies qui se situent en dehors de notre propre galaxie. Cependant, cette seule découverte n'aurait pas donné à Hubble la célébrité dont il jouit. C'est en mesurant la vitesse radiale des galaxies grâce à la spectroscopie qu'il a trouvé la loi qui a révolutionné l'étude de l'Univers. En effet, il établit que la vitesse d'éloignement des galaxies était proportionnelle à leur distance de la Terre. Il en déduisit une relation qui porte son nom. Il ne restait qu'un pas à franchir pour conclure que [l'Univers avait "débuté" en une formidable "explosion"] [...] C'est ce qu'on connaît maintenant sous le nom de théorie du Big Bang. Il n'est donc pas surprenant qu'à la suite de tous ces développements, Einstein ait dit un jour que l'invention de la constante cosmologique était la plus grande bévue de toute sa vie.
Cependant, cette théorie du Big Bang ne fut pas acceptée d'emblée par toute la communauté scientifique. Au contraire, plusieurs savants renommés lui opposèrent la théorie de l'état constant. Cependant, en 1965, la découverte du rayonnement cosmologique de fond apporta un appui important à la théorie du Big Bang et, aujourd'hui, la très grande majorité des savants l'acceptent.
Si l'Univers est maintenant en expansion, doit-on s'attendre à ce qu'il en soit toujours ainsi? La théorie du Big Bang n'entraîne pas nécessairement que l'Univers soit toujours en expansion. En effet, toute la matière de l'Univers est soumise à la force de gravité qui exerce une attraction sur toute cette matière en expansion et contribue à diminuer sa vitesse. Ainsi, le sort de l'Univers dépend de la quantité de matière qu'il contient. Plus la quantité de matière est importante, plus la force qui freine l'expansion est grande.
On envisage trois types d'avenirs possibles pour l'Univers. Dans le premier cas, si toute la matière existante dans l'Univers est inférieure à ce qu'on appelle la “masse critique”, l'Univers est destiné à croître indéfiniment. Si, par contre, la matière dans l'Univers est égale à cette “masse critique”, ses dimensions croîtront jusqu'à une certaine limite stable. Enfin, si la matière dans l'Univers dépasse la “masse critique”, l'Univers, après une longue période de croissance, commencera à se contracter et finira par avoir une dimension très petite, comme à l'origine.
Il est très intéressant de connaître [le contenu énergétique total] de l'Univers. [Les résultats de missions mentionnés plus haut, ainsi que ceux de la mission WMAP et des oscillations baryoniques, pointent vers un contenu dont les proportions relatives sont les suivantes: 5 % de matière ordinaire, 27 % de matière sombre et 68 % d'énergie noire.] […]
On a vu que la [relativité générale] joue un rôle primordial dans le modèle du Big Bang. S'il existe une force qui vient annuler cette force de gravité, il faudra réexaminer non seulement notre vision de l'avenir de l'Univers, mais également plusieurs éléments de la physique théorique. À la suite de la publication de ces résultats, doit-on s'attendre à un changement prochain de l'astrophysique? Va-t-on réintroduire la constante cosmologique? [Certains cosmologistes, comme Jean-Philippe Uzan, pensent qu'il est possible qu'on donne provisoirement des noms comme "énergie sombre" à des réalités qui nous échappent et que l'on doive peut-être remettre en question le Principe copernicien, donc que ce problème découlerait seulement d'un mauvais choix de symétrie.] Avant que de tels résultats ne soient admis par la communauté scientifique, ils seront examinés à la loupe et d'autres expériences seront entreprises pour les confirmer ou les infirmer. […]
M. Martin Rees, astronome royal à Cambridge, en Grande-Bretagne, fait un parallèle entre cette situation et celle dans laquelle se trouvait Kepler quand il essayait de décrire le mouvement des astres à partir de cercles, comme on le faisait depuis les Grecs. Ce n'est qu'après avoir reconnu que les astres se déplacent, non pas sur des cercles, mais sur des ellipses, qu'il a fait les découvertes auxquelles son nom est attaché.
J'ai choisi le titre de mon article en souvenir de l'abbé Thomas Moreux, qui avait exposé les connaissances de son temps sur le sujet (qui nous paraissent maintenant tout à fait désuètes) dans une série de volumes: “Qui sommes-nous?”, “D'où venons-nous?” et “Où allons-nous?”
Voir l'article : “Astronomers See a Cosmic Antigravity Force at Work” dans la revue “Science” du 27 février 1998 - Vol. 279, No 5355, pp. 1298-1299.
Portrait d'un trou noir
Mario Lessard - 2001 Révision 2016
Un des sujets les plus captivants et les plus spectaculaires de la science moderne est sans aucun doute celui des trous noirs et de leur "environnement". Les gens sont intrigués, mystifiés et veulent savoir s'ils existent vraiment.
Ces bêtes naissent d’une prédiction issue de la relativité générale d’Albert Einstein, mais avaient tout de même été imaginées dès le XVIIIème siècle par John Mitchell et Pierre-Simon de LaPlace comme explications à certains concepts astrophysiques qui suggéraient un champ de gravitation intense. Aujourd’hui, ces preuves indirectes de plus en plus "béton", et surtout suite à la détection directe des ondes gravitationnelles par la mission LIGO en février 2016, l’existence des trous noirs ne fait plus de doute. Depuis 2006, on considère 4 types de trous noirs selon leur masse: les trous noirs stellaires, les super-massifs, les intermédiaires et les primordiaux.
Dans cet article, je vous propose un portrait typique de ces monstres cosmiques suivant l’état actuel des connaissances. Nous allons aussi faire un voyage hypothétique au centre de la bête. Mais voyons d'abord un résumé de l'historique de ces phénomènes captivants.
SCHWARZCHILD
En 1915, en pleine guerre, un Allemand du nom de Karl Schwarzchild, trouva une solution exacte aux équations de la relativité générale d'Einstein, décrivant le champ gravitationnel d'une masse sphérique dans le vide, solution qui porte aussi le nom de "métrique de Schwarzchild". Cette métrique peut s'appliquer au Soleil et à son cortège planétaire et peut tout aussi bien décrire des effets subtiles comme la précession du périhélie de Mercure, que la théorie de Newton était incapable d'expliquer, et la déviation de la lumière d'une étoile aux abords d'une masse comme le Soleil. Donc, dans l'espace-temps de Schwarzchild, les planètes, la lumière d'une étoile, tout ce qui "gravite" suit simplement des trajectoires qu'on appelle géodésiques. Ces trajectoires nous paraissent circulaires parce que l'espace-temps est courbé par la masse et l'énergie. Le mouvement circulaire des planètes autour du Soleil n'est qu'une "illusion". Elles se déplacent plutôt en ligne droite – une géodésique, selon un principe de "moindre effort" – dans un espace-temps courbé par la masse et l'énergie du Soleil.
La solution de Schwarzchild a aussi une application universelle. Elle est indépendante de la nature de l'astre qui l'engendre. Elle ne dépend que de sa masse. C'est là que débute l’aventure. Prenons l'exemple du Soleil. Imaginons qu'une force comme l'implosion gravitationnelle comprime notre étoile. Sa masse serait confinée dans une sphère de plus en plus petite, à mesure que la compression s'effectuerait; sa densité augmenterait ainsi que son champ de gravitation. Il en va ainsi de la courbure locale de l'espace-temps qui s'accentuerait. Sa vitesse de libération augmenterait aussi. Présentement, elle est d'environ 600 km/sec. Mais si notre étoile était réduite à environ la moitié de sa taille actuelle, la vitesse de libération atteindrait des milliers de km/sec. Comprimons maintenant le Soleil jusqu'à ce qu'il ait un rayon de trois kilomètres. Ce rayon porte le nom de "rayon de Schwarzchild" pour le Soleil. La courbure de l'espace-temps atteint maintenant une valeur infinie (une singularité gravitationnelle) au centre de notre étoile. Sa vitesse de libération est maintenant de... 300 000 km/sec... la vitesse de la lumière.
Je rappelle que, selon la théorie de la relativité, rien ne peut voyager plus vite que la lumière. Ainsi, si le Soleil voyait son rayon comprimé jusqu’au rayon de Schwarzchild, sa vitesse de libération serait de 300 000 km/s et, en principe, il serait devenu trou noir. Rien, sauf la gravitation, ne pourrait plus s'en échapper. Par contre, les planètes continueraient d'orbiter autour de lui sans y être "aspirées", pourvu qu'il conserve sa masse. Ce n'est qu'en s'en approchant que l'on ressentirait l'immense effet de marée occasionné par la courbure spatio-temporelle.
LE NOIR ET LE DENSE
En 1939, Robert Openheimer établit que le scénario de la formation du trou noir "stellaire" est inscrit dans le destin d'une étoile massive lors de son effondrement gravitationnel. En effet, les réactions nucléaires au centre de l'étoile étant "éteintes", la pression thermodynamique ne vient alors plus compenser "l'étau" gravitationnel qui se resserre de plus en plus jusqu'à un point singulier nommé singularité. C'est là que certaines valeurs comme la courbure de l'espace-temps deviennent infinies. Si on trace une sphère imaginaire à partir du rayon de Schwarzchild autour de la singularité, on obtient une sorte d'horizon nommé "horizon des événements" qui est, comme son nom le suggère, la limite "physique" du trou, d'où il nous est impossible d'y voir ou d'en recevoir quoi que ce soit. C'est une sorte de cocon tissé par les trajets de la lumière "emprisonnée". Aussi, le trou noir ne peut qu'augmenter son aire de surface en "avalant" ce qui se trouve autour de lui. De taille stellaire de quelques masses solaires, il peut devenir un supermassif (comme celui qui est soupçonné dans le noyau de la galaxie M87), pourvu qu'il ait assez de matière à "bouffer". Contrairement à la croyance populaire, le trou noir n'est pas toujours quelque chose de très dense. Si notre trou noir d'une masse solaire requiert une densité "astronomique", un trou noir comme celui du centre de la galaxie d'Andromède serait seulement 200 fois plus dense que la Terre, et celui de M87, plus de 10 000 fois moins dense que l'eau. On pourrait voyager à l'intérieur pendant plusieurs heures sans être déchiquetés par l'effet de marée, mais rien ne nous empêcherait par contre de nous diriger vers la singularité une fois l'horizon franchi.
L'ESPACE ET LE TEMPS
Une fois l’horizon des événements franchi, les phénomènes prévus par la théorie dépassent l’entendement. Certaines des notions qui suivent sont pour le moins délirantes, mais sont tout de même issues des mathématiques associées. En effet, au fur et à mesure que l'on approche du trou, notre temps propre se "dilate". Notre unité de temps augmente. Cela est un principe de base de la relativité nommé : "décalage gravitationnel des fréquences". Si nous plongions vers le trou noir et qu'une personne demeurait à l'extérieur du trou (et assez loin) pour nous observer, elle nous verrait "ralentir" en approchant de plus en plus de l'horizon, jusqu'au moment où elle verrait une image de nous, "gelée" dans le temps. Mais pour nous, qui nous dirigeons vers le trou, nous verrions cette personne vieillir à vue d'œil et l'écoulement du temps extérieur se ferait de plus en plus vite par rapport au nôtre, à mesure que nous approcherions de l'horizon. On ne ressentirait absolument rien du changement. Pour nous, notre temps propre s'écoulerait normalement. Ce n'est qu'en regardant le monde extérieur que nous verrions un changement. Ces phénomènes sont illustrés dans le film "Interstellaire" de Christopher Nolan paru en 2014.
L'horizon des événements marque aussi la limite "statique" du trou. Dans notre monde extérieur, nous pouvons nous déplacer dans l'espace dans n’importe quelle direction. On peut aller à droite, à gauche, en avant, en arrière; rien ne nous en empêche. Mais le temps ne s'écoule que vers l'avenir. Il n'y a qu'une seule direction possible dans le temps. Le temps est la coordonnée directrice de notre espace-temps à nous. Impossible d'éviter la prochaine minute. Mais une fois traversée la limite statique, les coordonnées d'espace et de temps interchangent et c'est la coordonnée d'espace qui devient directrice. Cela s'appelle une singularité du genre espace. Cela est imposé parce qu'on ne peut avoir une position fixe à l'intérieur du trou. Maintenant, la singularité est inévitable. Essayer de s'en échapper, c'est comme essayer d'éviter la prochaine minute.
LE NOIR ET LE BLANC
Si on inverse la flèche du temps dans les équations de la relativité générale, on obtient un objet tout aussi fantastique que le trou noir: le trou blanc. Le trou blanc est l'inverse temporel des trous noirs. Rien ne peut sortir du trou noir; rien ne peut entrer dans le trou blanc. Le trou noir "aspire"; le trou blanc "expire". Certains cosmologistes pensent que le Big Bang est issu d’un trou blanc. Certains scientifiques ont aussi suggéré que l'on puisse entrer par le trou noir, emprunter ce qui s'appelle une gorge de Schwarzchild ou un trou de ver, et ressortir "ailleurs" dans un autre Univers ou dans le nôtre. Avouons cependant que ces trous blancs pourraient ne devoir leur existence qu’à une application naïve et hautement spéculative de la relativité générale. Mais est-ce que ce voyage serait possible? Hummm! Voyons voir...
LE VOYAGE
Dans les années 70, le mathématicien Roger Penrose a démontré que, dans le trou noir de Schwarzchild, le passage vers le trou de ver est bloqué par la singularité centrale. Donc, oublions cela, car nous serions écrabouillés. Cependant, il y a peut-être une alternative, car il est très peu probable que les trous noirs soient ceux décrits par Schwarzchild, ceux-ci sont sphériques et ne tournent pas. Or, les étoiles tournent bel et bien sur elles-mêmes et en plus, elles ne sont pas complètement sphériques. Comme la Terre, elles sont aplaties aux pôles. En 1962, Roy Kerr a trouvé une solution exacte aux équations de champs d'Einstein décrivant un trou noir en rotation. On les appelle "trous noirs de Kerr". Le trou de Kerr est bien différent de celui de Schwarzchild. Premièrement, il comporte non pas un, mais trois horizons. Un horizon externe, qui est la limite statique, un médian, qui est l'horizon des événements externes et un autre horizon des événements internes entourant la singularité. Cette singularité centrale n'a pas la forme d'un point comme dans le trou de Schwarzchild, mais plutôt celle d'un anneau.
Voici ce qui se passe, toujours selon Penrose, dans un trou de Kerr: ne fois la limite statique franchie, le temps se dilate. Une fois l'horizon des événements externes franchi, les coordonnées d'espace et de temps interchangent comme mentionné plus haut. Et une fois l'horizon des événements internes franchi, les coordonnées d'espace et de temps redeviennent comme à l'extérieur et la singularité est du genre temps. On peut alors naviguer aisément et même passer à travers la singularité pour se retrouver "ailleurs". Mais il faut prendre garde de ne pas la traverser par la tranche, sinon l’on serait englouti dans la singularité, tout comme dans la solution de Schwarzchild... Donc, selon Penrose, dans le trou de Kerr, on pourrait emprunter un trou de ver et ressortir par un trou blanc, vers "l'ailleurs".
Imaginons alors que nous possédions une technologie qui nous permettrait de propulser un vaisseau, avec une accélération constante et égale à celle de l'accélération gravitationnelle de la Terre, de 1 g. Ce serait très confortable pour le voyageur. Il s'approcherait alors graduellement de la vitesse de la lumière sans jamais l'atteindre. En plus, il bénéficierait de la dilatation du temps. À mi-chemin, il n'aurait qu'à décélérer au même rythme. On choisit sa destination, par exemple le trou noir de M87, situé à 50 millions d'années-lumière de la Terre et ayant une masse de 10 milliards de masses solaires, mais qui est peu dense, ce qui réduit le risque des effets de marées. Selon un petit calcul assez simple, il parviendrait à destination dans environ 34 ans de son temps propre. Par contre, il ne pourrait changer d'idée au bout du voyage, car plus de 80 millions d'années se seraient écoulées sur Terre. Comment alors pourrait-il nous faire partager son expérience? Parce que le trou de Kerr permet de franchir une distance "temporelle". Le trou de Kerr nous permet de bouger sur l'axe du temps autant que sur celui de l'espace (pourvu qu'on ne dépasse pas la vitesse de la lumière). Mais le retour est très aléatoire. Notre voyageur pourrait revenir par un trou de ver, mais se retrouver sur Sirius, ou encore sur Antarès. Rien, dans la théorie, n'indique ou ne renseigne sur l'issue du retour. Mais comme notre héros est très chanceux, il reviendrait au même endroit sur Terre, à environ une seconde après son départ. Il nous affirmerait être parti pendant 34 ans, mais pour nous, il serait parti depuis une seconde. Nous aurions bien du mal à le croire. Mais ses horloges, ainsi que ses rides ne mentiraient pas. Cela ne vous rappelle-t-il pas certains films comme "Contact" ou "Interstellaire"?!
Suggestions de lectures pour un public "primordial, stellaire et intermédiaire":
GREENSTEIN, Georges. Le destin des étoiles, 1987.
HAWKING, Stephen. Trous noirs et bébés Univers, 2000.
LUMINET, Jean- Pierre. Les trous noirs, 1987.
SUSSKIND, Leonard. Trous noirs – La guerre des savants, 2010.
Google est aussi votre ami.
Pour les "supermassifs":
HAWKING, Stephen et PENROSE, Roger. La nature de l’espace et du temps, 2003.
PEEBLES, P.J.E. Principles of Physical Cosmology, 1993.
HAARDT, Francesco & al. Astrophysical Black Holes, 2016.
CHOQUET-BRUHA, Yvonne et DAMOUR, Thibault. Introduction to General Relativity, Black Holes and Cosmology, 2015.
Lumières !!!!!
Mario Lessard - La Chronique de Mario, Mars 2003
Lumière...qui es-tu???
Donnez-lui l’aspect que vous voulez. Cela dépend du sujet traité. Donnez-lui la forme d’une onde lorsque vous parlerez du phénomène de la réfraction. Celle de rayons lorsque vous parlerez des trajets lumineux à l’intérieur de votre télescope. Et finalement celle de photons quand vous traiterez de l’effet photo-électrique sur un CCD. Toutes ces identités lui vont à merveille… elles sont toutes valides.
Au sens strict, la lumière n’est rien d’autre que de la radiation électromagnétique, et cette dernière est produite par des charges en mouvement accéléré. On doit à James Clerk Maxwell, au 19e siècle, le fondement théorique des phénomènes électromagnétiques. Maxwell fonda un système d’équations qui portent son nom (équations de Maxwell) et qui relient tous les aspects électriques et magnétiques dans la nature. Une de ces équations prévoit qu’un champ électrique variant en fonction du temps produit un champ magnétique et vice-versa. Cette grande généralisation d’une loi physique fut un bond de géant pour cette dernière, car il y avait longtemps que l’on cherchait le lien manquant entre l’électricité et le magnétisme.
Mais ce n’est pas tout. La vision de « géant » de Maxwell lui permit de prédire l’existence d’ondes électromagnétiques se propageant à une vitesse c… la vitesse de la lumière. Ultérieurement, un dénommé Hertz a réussi à produire ces ondes, et à prouver le fondement de Maxwell. Les ondes électromagnétiques sont donc formées d’une composante électrique, et d’une composante magnétique oscillant entre eux de façon orthogonale ou perpendiculaire et aussi à la direction de propagation de l’onde. Tout le spectre électromagnétique, des ondes gamma aux ondes radio, en passant par les rayons X, les rayons UV, la lumière visible et l’infrarouge, avec respectivement une augmentation de la longueur d’onde, obéit aux équations de Maxwell. C’est à cause de concepts comme la longueur d’onde, ainsi que la fréquence que nous pouvons déterminer si nous « voyons » cette lumière, et si c’est le cas, qui nous donnera aussi l’occasion de percevoir une sensation de couleur. Pour le sujet qui nous concerne, nous nous limiterons à la lumière visible (pour l’instant) qui n’est qu’une très petite « fenêtre » dans tout le spectre lumineux.
Petit photon…
Un photon est une particule d'énergie qui n'a pas de masse et qui se déplace très rapidement. Fait étrange d'ailleurs, un photon en mouvement a la particularité d'interagir avec la matière comme le fait une onde, c'est-à-dire comme une vague à la surface de l'eau. Puisque l'onde a à la fois une composante électrique et une composante magnétique, on parle « d'onde électromagnétique ».
Le messager de l’information électromagnétique, qui porte le « poids » énergétique de son origine sur ses épaules et qui le transmet dans tout l’univers, est le photon, ce petit paquet d’ondes. L’énergie d’un photon est proportionnelle à sa fréquence, et inversement proportionnelle à la longueur d’onde, le tout en relation avec une constante de la nature nommée constante de Planck et qui vaut 6,626 176 x 10 –34 Joules-secondes. Ainsi, un photon rouge est moins énergétique qu’un photon bleu. Donc pour qu’un faisceau de lumière rouge ait la même énergie qu’un faisceau de lumière bleue, il faut plus de photons.
L’énergie emportée par un photon est très petite. Quand on multiplie la constante de Planck par la fréquence disons d’un photon jaune, on obtient seulement une énergie de 3 dixième de milliardième de joules. Donc, faites le calcul, et vous verrez que dans le cas d’une ampoule de 100 watts, le nombre de photons émis par unité de temps est faramineux… tout près de 100 milliards de milliards chaque seconde !!!!
Personne n’a jamais vu de photons… Pour la même raison, l’œil ne « voit » pas l’illumination ou le flux de photons provenant de la source, mais voit plutôt la luminance, caractérisant la source qui reçoit le rayonnement. Le faisceau en forme de cône que l’on perçoit couramment lorsque l’on regarde en direction d’une source lumineuse est de la lumière diffusée et réfléchie par les agrégats de poussières de toutes sortes, et qui parvient à notre œil. Donc, lorsqu’on « allume » la lumière dans une pièce de la maison, pour « voir clair », les objets doivent d’abord être éclairés, pour ensuite nous « éclairer » à notre tour. Ce que l’on nomme aussi parfois, l’effet d’albédo.
 «Un photon est une particule d'énergie qui n'a pas de masse et qui se déplace très rapidement. Fait étrange d'ailleurs, un photon en mouvement a la particularité d'interagir avec la matière comme le fait une onde, c'est-à-dire comme une vague à la surface de l'eau. Puisque l'onde a à la fois une composante électrique et une composante magnétique, on parle « d'onde électromagnétique ».
«Un photon est une particule d'énergie qui n'a pas de masse et qui se déplace très rapidement. Fait étrange d'ailleurs, un photon en mouvement a la particularité d'interagir avec la matière comme le fait une onde, c'est-à-dire comme une vague à la surface de l'eau. Puisque l'onde a à la fois une composante électrique et une composante magnétique, on parle « d'onde électromagnétique ».
Source : http://astro-canada.ca/la_lumiere-light-fra
Ah !!!! ces grandeurs énergétiques et photométriques…
Brillance de surface, illumination, luminance, intensité énergétique, lux, lumens, candela… AAAARGH !!!! Il y a de quoi faire perdre la tête à n’importe qui. Révisons ici quelques définitions fondamentales en matière de photométrie et radiométrie, afin de faire un peu de ménage dans cette confusion. Cet exercice n’a qu’un but didactique et peut nous servir dans nos interprétations futures en termes de photométrie ou de radiométrie. À vous de juger si cela vous permettra de comprendre davantage. En astronomie on parle plutôt de magnitude et parfois de brillance de surface. Nous reviendrons sur ces deux concepts dans un prochain article.
Une source de rayonnement quelconque émet un champ de rayonnement autour d’elle. Si elle émet un flux égal dans toutes les directions, on dit que la source est isotrope. Par contre, s’il y a une direction de rayonnement privilégiée, par rapport à une autre, elle est alors anisotrope. Une étoile est considérée comme une source de rayonnement isotrope, et une nébuleuse planétaire, une source anisotrope. Parmi les grandeurs énergétiques utilisées, on distingue les grandeurs physiques qui décrivent la source de rayonnement, et celles qui décrivent la surface qui le reçoit. On parle aussi de radiométrie ou de photométrie. Radiométrie pour les grandeurs physiques ou absolues comme le watt/mètre carré ou encore en photons/stéradian/secondes, et photométrie pour les grandeurs photométriques du genre magnitude, lux, lumens, etc. en rapport de calibration spectrale sur la réponse de l’œil humain.
Grandeurs physiques décrivant l’émetteur
Flux énergétique
Exprimée en watt, c’est la puissance émise. Exemple : le Soleil émet 3.85 x 1026 watts, et une ampoule de 100 watts… 100 watts !!!
Énergie rayonnée
Exprimée en joule, c’est la perte d’énergie que subit la source qui rayonne. Exemple : l’ampoule ci-dessus, d’une durée de 1000 heures, aura rayonné 100 x 1000 x 3600 = 360 millions de joules. Comme exercice, faites le calcul pour le Soleil pendant 10 milliards d’années.
Intensité énergétique
Exprimée en watt par stéradian, c’est-à-dire le flux émis par une source ponctuelle, dans un angle solide donné. Si on reprend la même ampoule, son intensité énergétique est I = 100/4 pi = 8 W/sr.
Émittance énergétique
En watt/mètre carré. Le flux émit par un élément de surface donné. En général, cette grandeur ne correspond qu’à la moitié de l’espace traité. Si l’ampoule émet un flux des deux « côtés », on n’en considère qu’un seul. Exemple, soit r le rayon de notre ampoule, on a : 0,5 x flux énergétiques/4 pi r2 = émittance énergétique.
Grandeurs physiques décrivant une surface qui reçoit le rayonnement.
Éclairement énergétique
En watt/mètre carré. On l’appelle aussi, brillance, ou luminance. Semblable à l’émittance énergétique, mais cette dernière caractérise la source tandis que l’éclairement énergétique caractérise la surface qui reçoit la lumière.
Et pour terminer, décrivons brièvement quelques données photométriques couramment employées.
Le Lumen
L’unité de base du SI en photométrie, égale à un flux d’une Candela/stéradian. Un watt de lumière monochromatique à 550 nanomètres donne 680 lumens. Ce qui représente le seuil de vision photopique (vision de jour) de l’œil humain. Le seuil de vision scotopique (de nuit) à 510 nanomètres vaut 1720 lumens.
La Candela
Une mesure d’intensité. La candela est l’intensité lumineuse, dans une direction donnée, d’une source qui émet un rayonnement monochromatique de fréquence 540 x 1012 Hz et dont l’intensité énergétique dans cette direction vaut 1/680 watt par stéradian.
Le Lux
Le lux est l’éclairement d’une surface de un mètre carré recevant perpendiculairement un flux de un lumen. Une étoile de magnitude 0.0 éclaire l’atmosphère terrestre avec 2,5 x 10-6 lux.
Dans un langage plus familier aux astronomes amateurs, on connaît la magnitude, équivalent à une intensité ou à une émittance énergétique, et dont la grandeur radiométrique pourrait être le watt/mètre carré, et la brillance de surface qui désigne une intensité spécifique ou énergétique en watt/mètre carré/stéradian. Ces deux unités ajoutent de la confusion dans tout c’beau monde. Ce qui est important, c’est de les placer dans leur contexte. Avec un peu de pratique, vous y arriverez j’en suis sûr.
Un mot sur la brillance de surface en astronomie. Il existe une confusion fréquente concernant cette grandeur. Une question banale pourrait résumer : est-ce qu’un objet d’une brillance de surface donnée apparaîtra plus « brillant » dans un télescope ???? J’vous propose d’y penser.
Le mois prochain, on laisse de côté l’establishment physique, pis on parcourt un sujet plus terre à terre. On plonge dans le télescope pis on étudie le trajet et le comportement de la lumière qui y pénètre !!!
Références :
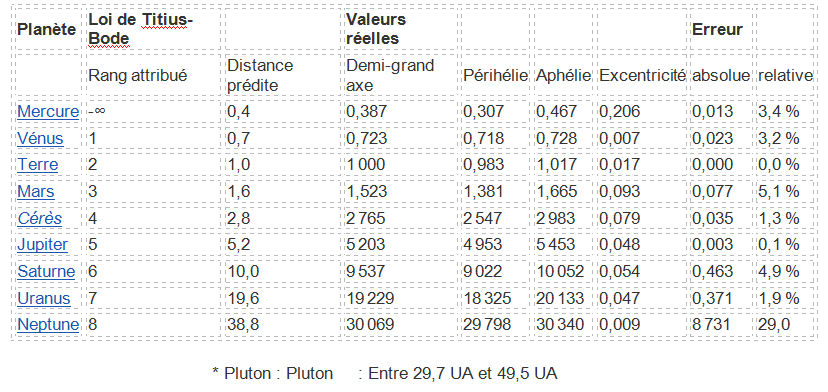
La Loi de Titius-Bode
Jean-Bruno Desrosiers
Je ne me souviens plus ou j’ai vu cette loi la première fois, mais ce fut pour moi un choc, presque une révélation. Que l’on puisse prédire la position des planètes du système solaire grâce à une petite formule toute simple...
L’histoire commence avec Johann Daniel Tietz (que l’on appelait aussi Titius), astronome allemand et professeur à Wittenberg. Il remarqua que cette séquence semblait expliquer la distance moyenne de chacune des planètes connues du Soleil. C’est au directeur de l’Observatoire de Berlin, Johann Elert Bode, que l’on doit d’avoir popularisé cette observation, connue sous le nom de règle Bode-Titius.
|
|
|
|
Johann Daniel Titius |
Johann Elert Bode |
Depuis les travaux de 1772 de l’astronome allemand Johann Elert Bode, tous les astronomes s’interrogeaient sur cette planète hypothétique : Bode avait en effet trouvé que les positions des planètes du système solaire connues à l’époque s’accordaient avec une loi empirique découverte en 1766 par le mathématicien Johann Daniel Tietz (qui signait ses travaux du pseudonyme latin Titius).
Il avait établi une relation entre les rayons des orbites planétaires. Cette relation a été ensuite validée par Herschel en mars 1781 par la découverte d’Uranus, ce qui poussa Johann Bode à rechercher la planète qui manquerait entre Mars et Jupiter.
La loi en pratique :
En prenant une suite de nombres de la suite de multiplication par 3 : 0, 3, 6, 12, 24, 48, 96, 192, en leur ajoutant 4 et en les divisant par 10, on obtient une nouvelle suite : 0,4 ; 0,7 ; 1 ; 1,6 ; 2,8 ; 5,2 ; 10 ; 19,6
Or il s’avère que l’échelonnement des distances au Soleil exprimées en unité astronomique (UA) des cinq planètes connues au milieu du XVIIIe siècle s’ajuste bien à cette dernière suite. Lorsque Titius publie en 1766 cette loi empirique, il ne manque à l’appel que deux planètes qui devraient se situer à 2,8 et 19,6 UA du Soleil.

(0 + 4) / 10=0,4 ---> Mercure : 0,39
(3 + 4) / 10=0,7 ---> Venus : 0,7
(6 + 4) / 10=1 ---> Terre : 1
(12 + 4) / 10=1,6 ---> Mars : 1,52
(24 + 4) / 10=2,8 ? : Céres : 2,8 UA, Vesta : 2,361 UA, Pallas : 2,77 UA et la ceinture d’astéroïdes entre Mars et Jupiter.
(48 + 4) / 10=5,2 ---> Jupiter : 5,2
(3 + 4) / 10=0,7 ---> Saturne: 9,55
(192 + 4) / 10=19,6 ---> Uranus : 1 9,6
(384 + 4) / 10=38,8 ---> Neptune : 30 069
(768 + 4) / 10=77,2 ---> Pluton : Entre 29,7 UA et 49,5 UA
Corroborée en 1781 par la découverte d’Uranus qui se trouve à 19,6 UA [selon la loi : (192 + 4) / 10 = 19,6], cette loi avait le vent dans les voiles jusqu’à la découverte de Neptune en 1846 par Urbain Le Verrier dont il a calculé les caractéristiques comme cause hypothétique des anomalies des mouvements d’Uranus. Cette planète était par contre de 30 UA du soleil et non à 38,8 UA comme le prédisait la loi de Titius.
Dans la zone des astéroïdes entre Mars et Jupiter (2-3 AU), on avait, en effet, imaginé une planète que l’on nomma Phaéton. Le courant de pensée actuel maintient que les astéroïdes de la ceinture principale sont les restes du disque protoplanétaire, l’accrétion en planète ayant été rendue impossible par les grandes perturbations gravitationnelles induites par Jupiter, pendant la période de formation du système solaire.
Par contre, en mars 2002, fut présentée une nouvelle théorie par les scientifiques de la NASA John Chambers et Jack Lissauer lors de la 33e « Lunar and Planetary Science Conference » en mars 2002. À partir de simulations, une telle planète aurait pu exister il y a environ 3,9 milliards d’années.
Conclusion :
Est-ce que la loi est bonne, mais qu’il y a eu des changements notoires dans le système solaire ?
Est-ce que le grand « Bombardement tardif » a pu créer ces différences ?
Ou est-ce que cette loi n’est qu’une curiosité et que les distances font partie des hasards que la science ne peut expliquer ?
Nous le verrons sans doute lors des prochaines découvertes en exoplanètes !
C’est fou, non ?
Jean-Bruno Desrosiers
Astro Info, hiver 2018
Lectures suggérées et références :
http://www.cosmovisions.com/Titius.htm
https://fr.wikipedia.org/wiki/Johann_Daniel_Titius
https://fr.wikipedia.org/wiki/Loi_de_Titius-Bode
https://fr.wikipedia.org/wiki/Urbain_Le_Verrier
https://fr.wikipedia.org/wiki/Phaéton_(planète)
https://fr.wikipedia.org/wiki/Némésis_(étoile_hypothétique)
http://www.messagetoeagle.com/mystery-of-planet-v-was-there-once-a-5th-planet-between-mars-and-the-asteroid-belt/
Les Céphéides : Calculer les distances grâce aux pulsations d'une étoile (module de distance)
Jean-Bruno Desrosiers - Décembre 2020
|
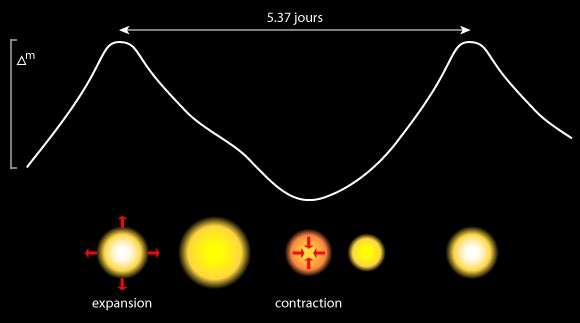
Les Céphéides et les pulsantes intrinsèques. Elles semblent vivre et battre comme un cœur au repos... |
 |
Henrietta Swan Leavitt (1868-1921), qui a percé leurs mystères, a pu trouver une méthode d’évaluation des distances. |  |
 |
Elles ont permis à Edwin Hubble de comprendre que la grande « nébuleuse » d’Andromède était une galaxie hors de notre propre galaxie. Magie ! |  |
En fait... non. Les Céphéides sont en réalité un passage, une phase que certaines étoiles traversent. Leurs fusions en leurs cœurs créent des pulsations de ses couches supérieures. |
Une Céphéide est une étoile de 4 à 15 fois plus massive que le Soleil et de 100 à 30 000 fois plus lumineuse, dont l’éclat varie de 0,1 à 2 magnitudes selon une période bien définie, comprise entre 1 et 135 jours. Elles ont quitté la séquence principale et traversent la bande d’instabilité due à son hélium qui devient prédominant dans son cœur et qui commence à produire du carbone ce qui provoque ces pulsations si régulières.
|
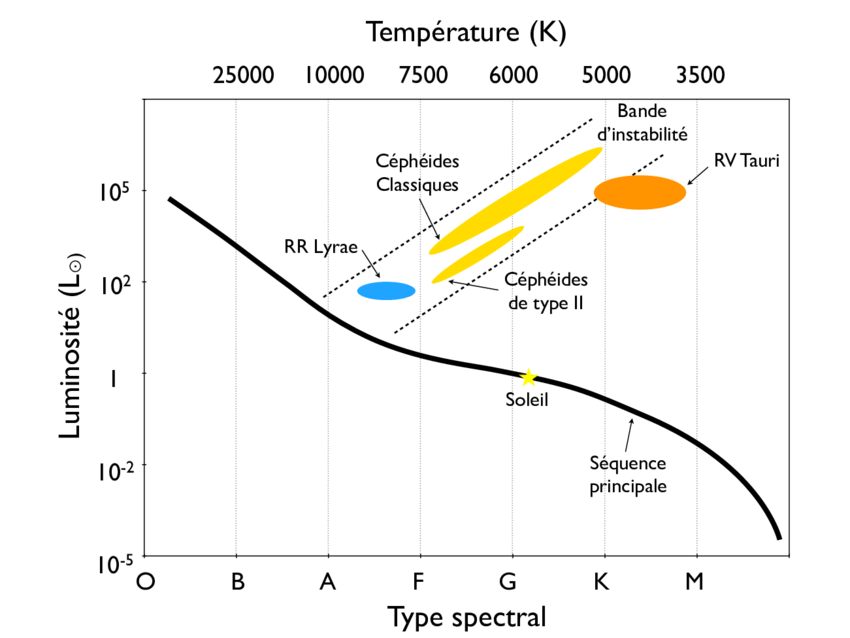
Au cours de son cheminement, elle fera des passages d’un côté et de l’autre du diagramme HR. Le mystère de la fréquence de ces pulsations réside aussi dans leurs volumes, car plus elles sont lumineuses, plus leurs pulsations seront lentes. |
 |
||
 |
C’est à Arthur Eddington (1926) que l’on doit l’explication de ces pulsations baptisées par l’effet de « Valve d’Eddington ». C’est grâce à l’hélium que les Céphéides pulsent régulièrement. L’hélium dégradé dans le cœur de l’étoile est ionisé plusieurs fois ce qui la rend plus opaque. La chaleur reste alors captive. Un cycle prend alors forme, plus l’étoile se compresse et donc se réchauffe. |
« À un moment donné, lors de son expansion, elle se refroidit et tend à reprendre sa forme première et le cycle recommence. La fréquence dépend de la masse de l’étoile, plus elle est petite, plus la fréquence sera rapide et l’inverse quand sa masse est plus grande.
C’est avec des tables statistiques basé selon leurs fréquences de pulsation que l’on peut obtenir simplement en les observant. Leurs fréquences sont directement reliées à la masse de l’étoile cible qui est le produit de sa masse volumique moyenne ρ, par son volume (M = ρ V).
Donc, à partir de ces tables statistiques et de leurs magnitudes apparentes (en filtre V), on peut en déduire leurs magnitudes absolues. Il ne restera plus qu’à appliquer le calcul du module de distance qui nous donnera alors la distance de l’étoile. Les Céphéides sont donc des indicateurs de distance très cool, aussi appelés “chandelles standards”.
*Une attention doit être portée, car d’autres variables pulsantes sont aussi dans la bande d’instabilité : W Virginis (Céphéides type II) et les RR Lyrae.
Ce sont des Céphéides aussi, mais de type II, autrement dit, de vieilles étoiles avec taux plus faible de métaux et généralement moins massives que les Céphéides de type I. Périodes plus longues et souvent on les rencontre dans les amas globulaires. Les RR Lyræ ont pour leur part des périodes beaucoup plus courtes, et dont le type spectral est A pour la plupart. On les rencontre la plupart du temps dans les amas d’étoiles (M3, M13...) »
Toutes ces familles de « pulsantes intrinsèques » ont toutes un point en commun, elles sont des chandelles utilisables pour calculer les distances selon leurs fréquences de pulsations.
Aussi, quelques faits intéressants sur les Céphéides qui sont dans les 100 milliards d’étoiles de notre Galaxie :
- Les Céphéides sont peu nombreuses ~ 1 000 Céphéides répertoriées actuellement
- Mais environ 20 000 à 35 000 Céphéides suspectées
- 5 000 et + pourraient être découvertes par la mission Gaia de l’ESA
- 40 Céphéides seraient visibles à l’œil nu (parmi les 6 000 étoiles)
- L’Étoile Polaire est la Céphéide la plus proche de nous et la plus brillante (431 a.l.)
https://fr.wikipedia.org/wiki/Alpha_Ursae_Minoris
Comment utiliser le module de distance pour les céphéides de type classique (DCEP) ?
1- Il faut la magnitude observée en filtre « V »
2- Il faut la fréquence en jour, car on peut alors avoir la magnitude absolue (magnitude de l’étoile vue à 10 parsecs de nous) grâce à un calcul : Mv ≃-2,76 log10 Pd - 1,40.
*Il y a aussi un site qui facilite ce genre de calcul :
http://eguruchela.com/physics/calculator/Absolute-Visual-Magnitude-of-Cepheid-Variables-Calculator
3- À partir de là, on peut obtenir la distance mathématiquement grâce au module de distance.
Par exemple :
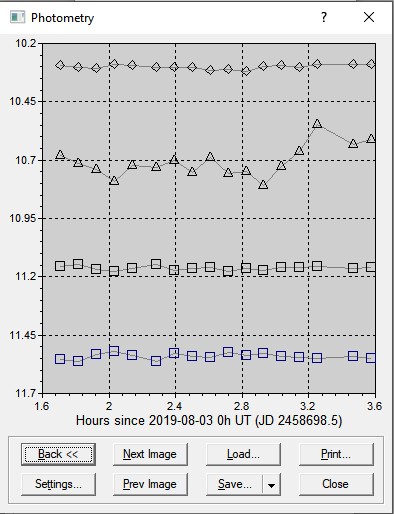
Prenons une céphéide connue : RX Cam, sa variation est de 7,3 - 8,07 en filtre V. Selon le VSX de l’AAVSO, cette céphéide à une période de 79 120 jours. Selon mes observations en filtre V, j’obtiens une moyenne de magnitude apparente de 7 904. Ma formule sera alors : d (en PC) =
| Donc : |
Donc : |
Donc : |
Donc : |
22 732 856 PC X 3.26 (pour la conversion en années-lumière)= 7 410 911 AL
Bien sûr, ce calcul n’est qu’approximatif et les critères de qualité photométrique doivent être bien appliqués sur plusieurs observations et plusieurs observatoires. Son type d’étoiles est d’abord une « variable », donc à moins de disposer de matériel professionnel, on peut donc difficilement arriver avec un chiffre précis. Mais on peut quand même considérer cette approche mathématique comme très « intéressante ».
De plus, ce module de distance peut s’appliquer aux étoiles RR Lyrae, car on sait qu’en moyenne, ces étoiles ont une magnitude absolue relativement stable variant entre 0,6 et 0,7.
Même les supernovas de type 1a qui sont reconnues pour avoir une magnitude absolue de -19,3 (à 1/4 de magnitude près), car le mécanisme qui la produit est dû à un seuil de masse et elles peuvent donc aussi profiter de ce module afin de connaître leurs distances lors que l’on est au tout début de l’évènement, enfin à son maximum.
En fait, ce qu’il faut retenir, c’est qu’avec le simple calcul du module de distance, dès qu’on a la magnitude absolue (magnitude d’une étoile à 10 parsecs) et la magnitude précise (en filtre V), on peut obtenir une distance.
Encore une fois, pour une certaine précision, il faut prendre plusieurs relevés, et ce, par plusieurs observateurs et l’on fait une moyenne. Mais c’est tout de même une autre curiosité à expérimenter !
Références :
https://fr.wikipedia.org/wiki/Henrietta_Swan_Leavitthttps://fr.wikipedia.org/wiki/Expansion_de_l%27Univers
https://astronomia.fr/3eme_partie/variables/varPeriodiques.php
http://www.astrosurf.com/saml/ACCUEIL_suite_1_files/Diaporama%20ce%CC%81phe%CC%81ides_version%20finale_20170715.pdf
https://astronomia.fr/3eme_partie/etoiles_java/calculette.php# :
https://fr.wikipedia.org/wiki/Module_de_distance
https://www.futura-sciences.com/sciences/definitions/astronomie-cepheide-6438/
Sylvie Beaulieu, responsable de l’Observatoire du Mont-Mégantic : http://omm.craq-astro.ca/
Les calendriers
Robert Véronneau
Depuis les débuts de l'Histoire, on a dû trouver une façon de calculer le temps. Bien évidemment, les jours furent les plus faciles à compter: il était évident de les voir défiler. On pouvait voir le début du jour au lever du Soleil et sa fin à son coucher. Lorsque le Soleil était au zénith, c'était le milieu de la journée. Mais pour de longs intervalles de temps, il devenait difficile de compter les jours. On préférait alors parler de saisons, de lunaisons, et même d'années (par exemple, je suis né il y a 31 étés -ceci correpond au moment où j'ai écrit ce texte...)
Pour une conversation de tous les jours, c'était suffisant, mais avec l'avènement du commerce, des sciences et la transcription de l'Histoire, on a senti le besoin d'avoir un moyen plus précis de calculer et de prévoir le temps. On a donc inventé les calendriers.
Les jours se sont imposés tout de suite comme étalon de mesure des calendriers. On les a donc conçus à partir de ceux-ci. Évidemment, comme on comptait déjà les " Lunes ", celle-ci devint aussi une référence pour les mois. L'intervalle de temps entre deux nouvelles Lunes (révolution synodique) est de 29 jours 6 heures à 29 jours 20 heures, pour une moyenne de 29 jours 12 heures 44 minutes. On connaissait aussi le temps d'une révolution du Soleil autour de la sphère céleste (l'année), soit 365 jours 5 heures 48 minutes 46 secondes ou 365,2422 jours. La Lune accomplit en moyenne 12,37 révolutions pendant cet intervalle.
Calendriers lunaires :
Les premiers calendriers connus furent tous lunaires, c'est-à-dire qu'on se basait sur les mouvements de la Lune pour les établir. Ainsi, les Babyloniens, les Égyptiens, les Grecs, les Chinois, les Romains et plusieurs autres peuples ont établi leurs premiers calendriers avec la Lune comme référence. À l'heure actuelle, le calendrier musulman et certains calendriers africains sont toujours établis suivant les mouvements de la Lune. Les mois de ces calendriers commençaient généralement à la Nouvelle Lune. Comme, à l'époque, on ne maîtrisait pas tout à fait les calculs de l'orbite lunaire, on faisait coïncider le premier jour du mois avec la première apparition de la Lune le soir. Et, vu que l'orbite lunaire ne durait pas un nombre de jours exacts, on devait faire alterner des mois de 29 et de 30 jours. Une année comportait alors 12 mois, mais comme 12 mois lunaires ne donnent que 354 jours environ, les saisons retardaient par rapport au calendrier. On eut donc l'idée d'y inclure un 13e mois au besoin.
En 432 Av. J.-C., l'astronome Méthon d'Athènes découvrit un multiple commun aux durées de l'année et des lunaisons: 19 années de 365,25 jours valent 6939.750 jours alors que 235 lunaisons donnent 6939.688 jours, soit une différence d'une heure 29 minutes pour l'intervalle. Pas si mal!
Comme 235 lunaisons donnent 19 années de 12 mois lunaires plus 7 mois, on n'avait plus qu'à répartir ces 7 mois durant ces 19 années. Cela ne laissait plus qu'une erreur d'un jour tous les 320 ans. Ce cycle de Méthon est encore utilisé aujourd'hui dans le calendrier Hébraïque.
On doit aux Chaldéens la semaine de 7 jours correspondant aux quartiers de la Lune. On leur doit aussi les noms des jours d'après les planètes: dimanche pour le Soleil (Sunday), lundi pour la Lune (Lunae dies -Monday), mardi pour Mars (Martis dies), mercredi pour Mercure (Mercurii dies), jeudi pour Jupiter (Jovis dies), vendredi pour Vénus (Veneris dies) et samedi pour Saturne (Saturni dies -Saturday).
Les Égyptiens, peuple d'agriculteurs, furent les premiers à abandonner la Lune comme base de leurs calendriers. Ils désiraient faire concorder le calendrier avec le temps des semailles et des moissons. Ils fixèrent la durée du mois à 30 jours sans plus s'occuper des phases de la Lune. Ils ajoutèrent 5 jours complémentaires à la fin du 12e mois pour compléter une année de 365 jours. On savait que l'année vraie était un peu plus longue et on avait calculé que le premier de l'an passerait par toutes les saisons pour revenir à son point de départ en 1460 années. On appelait cette période l'année Sothiaque.
Les Romains eurent d'abord un calendrier fait de 10 mois lunaires. Cela donnait une année de 295 jours. Ces mois étaient: martius, aprilis, maius, junius, quinctillis, sextillis, september, october, november et december. On ajouta ensuite à l'année les mois de janvier et de février afin d'avoir une année plus équilibrée. Cela donnait une année de 354 jours. Pour remédier à ce problème, on introduisait un mois supplémentaire de temps à autre.
À l'époque les calendriers étaient de juridiction régionale ou municipale. Un grand prêtre ou un notable de la ville devait surveiller la Lune et déclarer qu'un nouveau mois commençait. Il devait aussi décider quand on devait ajouter un 13e mois. Une ville ou une région n'avait pas nécessairement la même date qu'une autre. Cela donnait lieu à beaucoup de confusions dans la tenue d'actes notariés ainsi que lors de la rédaction de contrats. Sans compter que certains hommes d'affaires peu scrupuleux profitaient de cette confusion et quelquefois se permettaient d'influencer les décisions du Grand Prêtre à leur avantage.
Jules César :
C'est alors que Jules César ordonna la réforme du calendrier. Il demanda à l'astronome Sosigène d'Alexandrie de lui concevoir un calendrier qu'il pourrait imposer à tout le monde. On établit d'abord l'année à 365 jours en distribuant des jours supplémentaires à chaque mois. On eut alors des mois de 30 et de 31 jours, sauf pour février, le dernier mois de l'année, qui resta à 29 jours. Chez les Romains, on croyait que février était un mauvais mois et on ne voulait pas l'allonger. On établit ensuite qu'à tous les 4 ans, on ajouterait une journée au mois de février afin de donner une année moyenne de 365.25 jours. On donna le nom de bissextiles à ces années.
À l'époque on séparait les mois en 3 sections : les calendes (5), les nones (13) et les ides (21). Les jours se comptaient à partir de ces divisions, out comme pour l'heure sur une horloge: midi moins 5, par exemple. Le 28 février était alors le 6e jour avant les calendes et lors d'une année bissextile, on répétait deux fois ce jour, d'où l'expression bissextile.
Les changements prirent effet le 1er janvier de cette année et marquèrent le début de la nouvelle année julienne. César fut tellement fier de son calendrier qu'il donna son nom au mois quinctillis qui devint alors julius (juillet). Après l'assassinat de César par son fils Auguste, ce dernier, devenu empereur et espérant avoir le même prestige que son illustre père, ordonna qu'on change le nom du mois sextillis pour le nom d'Augustus. Il ordonna aussi qu'on enlève un jour à février et qu'on le donne à Augustus pour qu'il ait le même nombre de jour que Julius. Ce calendrier que l'on connaît bien fut imposé partout dans le monde.
La réforme du pape Grégoire :
En 1582, le pontife Grégoire ordonna qu'on réajuste le calendrier avec le Soleil. En effet, l'année vraie durant 365,2422 jours, il y avait une différence de 11 minutes avec l'année julienne. À l'époque de Grégoire, le calendrier avait pris un retard de 10 jours sur le Soleil. On croit que Grégoire s'inquiétait de voir Pâques (la mort du Christ) s'approcher de plus en plus de Noël (la naissance du Christ). Il décréta donc que le 4 octobre 1582 sera suivi du 15 octobre 1582. Pour éviter qu'une pareille situation se répète, il commanda aux astronomes Lilio, Clavius et Chacon d'établir la durée exacte de l'année et de trouver une méthode pour ajuster le calendrier à cette dernière. L'erreur entre le calendrier Julien et le Soleil était d'environ 3 jours sur 400 ans. On décréta donc que les années séculaires (siècles) ne soient bissextiles que si elles se divisaient par 400. Il reste toujours une erreur à ce calendrier d'environ 1 jour sur 3 000 ans. C'est toutefois suffisant pour l'instant. La majorité du monde se conforma peu à peu à ce calendrier qu'on utilise toujours aujourd'hui.
La révolution française :
Suite à la révolution, les révolutionnaires français inventèrent un nouveau calendrier: le Calendrier républicain. Il comportait 12 mois de 30 jours, les jours à l'intérieur d'un mois étaient séparés en 3 décades: primidi, duodi, tridi, quatridi, quinquidi, sextidi, septidi, octidi, nonidi, décadi). Les mois étaient séparés en trimestres évoquant les saisons. Voici leurs noms: début d'année l'automne: vendéminaire, brumaire, frimaire; l'hiver: nivôse, pluviôse, ventôse; le printemps: germinal, floréal, prairial.; l'été: messidor, thermidor, fructidor. On ajoutait aussi 5 jours complémentaires après le 12e mois (6 durant les années bissextiles). Ces jours devaient servir pour fêter la République. Ce calendrier avait l'avantage de faire concorder le début et la fin des mois avec les fins de semaine. On pouvait alors mieux établir les dates de différents événements (finance, école, contrats, etc.). Le 22 septembre 1792, jour de la proclamation de la République, à l'équinoxe d'automne, devint alors le 1er vendéminaire de l'an 1.
Les gens, à l'époque, eurent beaucoup de difficulté à s'adapter à ce calendrier et Napoléon l'abolit 13 ans plus tard.